最終更新日

温度計保護管の強度計算

温度計 計装

温度計保護管の強度計算の方法について解説します。従来の基準であったASME PTC 1974と現在、日本国内での設計指針とされるJSME S012-1998の内容を紹介します。

保護管強度計算の目的

流体が流れる配管に温度計を挿入すると保護管の下流にカルマン渦が発生します。このカルマン渦による強制振動数と保護管の固有振動数が一致すると共振（同期振動）が発生します。共振時は非常に大きな振動が発生するため、これによって保護管折損するおそれがあります。したがって、温度計設計時には保護管の固有振動数（寸法、仕様）に問題がないか十分に検討しなければなりません。

温度計保護管の強度計算の歴史

1960年代

国内外プラントにおいて温度計保護管の折損の事例が発生していましたが、この頃は保護管強度計算に関して標準となる設計指針はまだない時代でした。折損原因は主にカルマン渦の振動によるものでした。

1970年代

ASME PTC 1974（米国機械学会）が発行される。国内プラントでもこれを基にして保護管の強度計算が行われるようになる。

1990年代
  • 1995年：高速増殖炉もんじゅで熱電対保護管の折損によるナトリウム漏洩事故が発生。
  • 1998年：もんじゅの事故を契機に JSME S012-1998: 配管内円柱状構造物の流力振動に関する評価指針（日本機械学会）が発行される。
2010年代
  • 2010年：ASME PTC TW-2010: Thermowells Performance Test Codes（米国機械学会）が発行される。ASME PTC 1974から全面的に見直された内容。JSMEと同様に抗力方向の振動を考慮した内容。また、保護管の固有振動数の計算式がより精密に定められている。
  • 2016年：ASME PTC TW-2016が発行。

ASME PTC 1974の評価条件

判定条件：カルマン渦による強制振動数fsと保護管の固有振動数fnが以下の関係を満たすこと。

\dfrac{f_{s}}{f_{n}} \lt 0.8

要するに流体のカルマン渦による強制振動数fsが、保護管固有振動数fnの8掛けした数字より小さければOKということです。逆に言うと保護管の固有振動数が十分に大きければ共振が発生しないのでOKということです。

カルマン渦の強制振動数計算式

f_{s} = St \dfrac{V}{D} \times 10^{3}
St：ストローハル数 [-]
V：流速 [m/s]
D：保護管外径 [mm]

ストローハル数はカルマン渦の振動の周波数を表す無次元数です。ストローハル数はレイノルズ数によって変化しますが、円柱形の保護管の場合、約0.2で一定となります。

【参考】カルマン渦列 [JSME Mechanical Engineering Dictionary]
https://www.jsme.or.jp/jsme-medwiki/09:1002355

保護管の固有振動数計算式

f_{n} = \dfrac{1.875^{2}}{2 \pi L^{2}}\sqrt{\dfrac{EI}{\rho A_{s}}\times 10^{12}}
L：保護管長さ [mm]
E：材料ヤング率 [N/mm2]
I：断面二次モーメント [mm4]
ρ：材料密度 [kg/m3]
As：保護管断面積 [mm2]

上記計算式はストレート形保護管の計算式です。先端が細くなるテーパ形保護管の固有振動数は非常に複雑な計算式になります。詳細はJSME S012-1998やASME PTC TW-2016(2010)に記載されています。テーパ形はJSMEとASMEでも計算式が異なります。テーパ形は先端が細い形状になっているのでストレート形に比べて固有振動数が高くなります。したがって、主蒸気ラインのように共振を回避したいケースでは一般的にテーパ形の形状が採用されます。

もんじゅの温度計保護管の問題点

もんじゅの温度計保護管はASME PTC 1974の基準をクリアしており実際の fs/fn比は0.8未満でした。しかし、ここで見落とされていたのが、fs/fn < 0.8の領域においても同期振動が発生するケースがあるということです。

実はASME PTC 1974には致命的な問題点があり、交互渦による揚力方向（流れに垂直な方向）の振動は考慮していますが、抗力方向（流れ方向）の振動（インライン振動）は考慮されていませんでした。なのでASME PTC 1974での計算結果上はOKでも、もんじゅでは抗力方向の振動によって保護管が折損してしまったというわけです。

※実際にはASMEには抗力方向の振動に関する規定が1991年に追加されていました。ただし、ASMEの全面的な見直し改訂がされるのは2010年になってからです。

JSME S012-1998の評価条件

もんじゅの保護管折損を契機として強度計算の見直しが実施され、日本機械学会から強度計算の設計指針が発行されました。JSMEでは以下の評価を共に満足すればその保護管は使用可能と判定します。1つ目が同期振動に関する評価で、2つ目は保護管に働く応力の評価です。

  1. 同期振動の回避または抑制評価
  2. 流体振動に対する強度評価

同期振動の回避または抑制評価

2つの評価パラメータ（換算流速Vrと換算減衰率Cn）を計算して、使用する保護管が下図に示す(a), (b), (c)いずれかの領域に入っていればOKです。

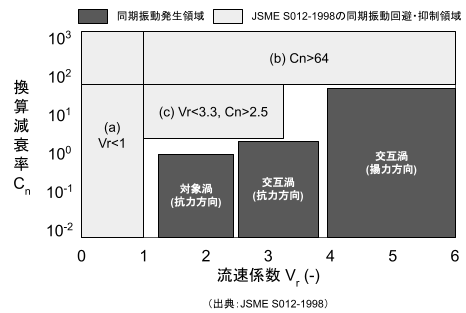
(a), (b), (c)それぞれの説明は以下の通りです。

(a) 固有振動数に対して強制振動数が十分に低く、揚力方向・抗力方向どちらの同期振動も回避している。
(b) 振動の減衰が十分に大きいため、同期振動が抑制されている。※振動数が一致（共振）しても応力が極めて小さいため問題ないとしている。
(c) 揚力方向（流れに垂直な方向）の同期振動は回避できている。抗力方向（流れに平行な方向）の同期振動は減衰によって抑制されている。

JSME S012-1998では、ASME PTC 1974で考慮していなかったfs/fn<0.8を考慮しています。また、fs/fn≧0.8の領域においても減衰が十分に大きければ強度的に問題ないとして使用可能としています。

換算流速Vr

V_{r} = \dfrac{V}{f_{n} D} \times 10^{3}
V：流速 [m/s]
fn：保護管の固有振動数 [Hz]
D：保護管外径 [mm]

換算流速Vrは保護管の固有振動数fnに対してどの程度の流速が流れているかを表す無次元数のパラメータです。流速Vとストローハル数Stによって強制振動数fsが決まるので、結局は換算流速Vrというのは fs/fn比と同じ考え方です。Vrが小さいということはfs/fn比が小さい（＝固有振動数fnに対して強制振動数fsが低い）ということです。

換算減衰率Cn

C_{n} = \dfrac{2m \delta}{\rho D^{2}} \times 10^{6}
m：保護管質量 [kg]
δ：対数減衰率 [-]
ρ：材料密度 [kg/m3]
D：保護管外径 [mm]

対数減衰率δと減衰比ζ

対数減衰率 \delta = 2 \pi \zeta であり、ζ は減衰比 (Damping factor) です。要は振動の減衰の大きさを示す値ですが、これは一意的に決まる値ではないし簡単に測定できる値でもありません。また、保護管の取付方法（フランジ、ネジ、溶接）によっても変わってきます。

参考値として、JSME S012-1998では ζ=0.005 が使われています。一方でASME PTC TW-2016(2010)では ζ=0.0005 としています。ζ が一桁変わると換算減衰率Cnも一桁変わるので要注意です。ζ が小さいほどCnも小さくなる（＝判定NG側に行く）ので、ASMEのほうがより厳し目に見ていることになります。

以上がカルマン渦による同期振動に関する評価でした。次に、保護管に働く応力の評価について記載します。

流体振動に対する強度評価

判定基準：以下の応力を組み合せた応力が保護管材質の許容応力以下であること。

  1. 定常抗力による応力σD
  2. ランダム振動応力σR
  3. 配管内圧力による圧縮応力σP

合成応力が保護管材料（SUS304やSUS316L）の許容応力以下であればOKと判定します。実際の検討ではσRは超複雑なので無視して、σDとσPだけで検討するケースがほとんどではないでしょうか。σDとは流体により保護管が受ける抗力Fによって保護管根元に働く曲げ応力のことです。σDとσPの計算方法を下記に記載します。

流体より保護管が受ける抗力F [N]

F = C_{D} \dfrac{\rho}{2} V^{2} A \times 10^{-6}
CD：抗力係数 [-]
ρ：流体密度 [kg/m3]
V：流速 [m/s]
A：投影面積 [mm2]

投影面積とは保護管が流体を受ける面積、つまり保護管の外径×実挿入長のことです。抗力係数CDはレイノルズ数に依存します。ただし、 Re = 2 \times 10^{4} \sim 2 \times 10^{5} の範囲では CD=1.2 でほぼ一定です。

曲げモーメントM [N・mm]

M = F \left( L - \dfrac{L_{A}}{2} \right)
L：保護管長さ [mm]
LA：実挿入長 [mm] （配管に入っている部分の長さ）

上の計算式では抗力Fが挿入部分の中心部に集中して加わる力としています。

円柱の根元部分に発生する曲げ応力σD [N/mm2]

\sigma_{D} = \dfrac{M}{Z}
M：曲げモーメント [N・mm]
Z：断面係数 [mm3]

外圧により円柱に発生する圧縮応力σP [N/mm2] 

\sigma_{P} = \dfrac{2 D_{o}^{2}}{D_{o}^{2} - D_{i}^{2}} P
Do：保護管外径 [mm]
Di：保護管内径 [mm]
P：圧力 [MPa]

これらの応力を計算して、保護管材料の許容引張応力以下であればOKという具合です。

まとめ

温度計保護管の強度計算の方法について解説しました。「愚者は経験に学び、賢者は歴史に学ぶ」という有名な言葉がありますが温度計の保護管折損は「もんじゅ」だけではなく世界中のプラントで起こっている事例です。大抵の事例は強度計算を怠った結果、起こっているケースが多いです。正直、レイノルズ数の計算とかまぁまぁ面倒なのですが、設計ミスでモノが壊れるのはそれの1000倍大変なので設計時に固有振動数と強制振動数を計算して問題ないかちゃんと確認するようにしましょう。特に細くて長い保護管は固有振動数が低くなるので注意が必要です。

参考サイト