電験2種（令和5年度）合格体験記

電験2種二次試験に合格しましたのでこれまで内容を振り返ってみます。

電験2種を受験する理由

電気エンジニアとしてレベルアップしたい、知識を向上させたいという思いから受験を決意しました。また、電験2種が必要な仕事ではないのですが、2種は社内的に非常に強いアピールポイントになるのでそれも1つの動機でした。

合格までの流れ

2021年：2種受験を決意して一次試験の勉強を開始。
2022年：一次試験「理論」「機械」「電力」 合格、「法規」受験せず。
2023年：一次試験「法規」合格、二次試験合格

1年で一発合格するつもりはさらさらなく、2ヶ年計画で合格する計画でした。理由として、2年計画であれば二次試験に全力で望むチャンスが2回あるからです。1年目で一次試験4科目とってそこから二次試験の勉強を始めて合格するのは可能性として低いので、初めから2年計画で行きました。

一次試験の得意科目である理論と機械で9割以上を取れたことは二次試験への自信に繋がりました。

カフェジカ自己採点
理論→9割超えで楽勝💪
電力→60点超えてるので大丈夫なはず。
機械→あんまり自信なかったけど9割超え。ツイてる😙
この成績なら2ヶ年計画にしなくても良かったかも？

— hyperkomatty (@komatty_denki) 2022年8月20日

二次試験振り返り

二次試験の内容を振り返ってみます。以下の問題のタイトルは 電験王2 から引用させていただきました。

電力・管理科目

問1    圧力トンネルを伴うダム水路式発電所における水撃作用に関する論説問題    水力
問2    多導体送電線の利点とその理由に関する論説問題    送電
問3    等面積法を用いた過渡安定性に関する計算問題    送電
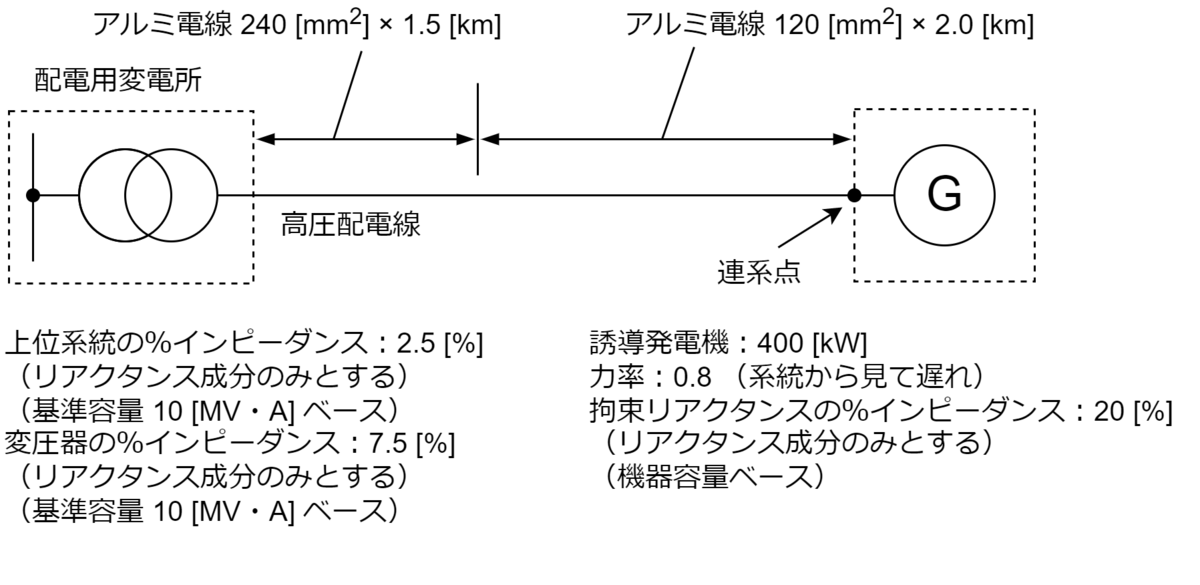
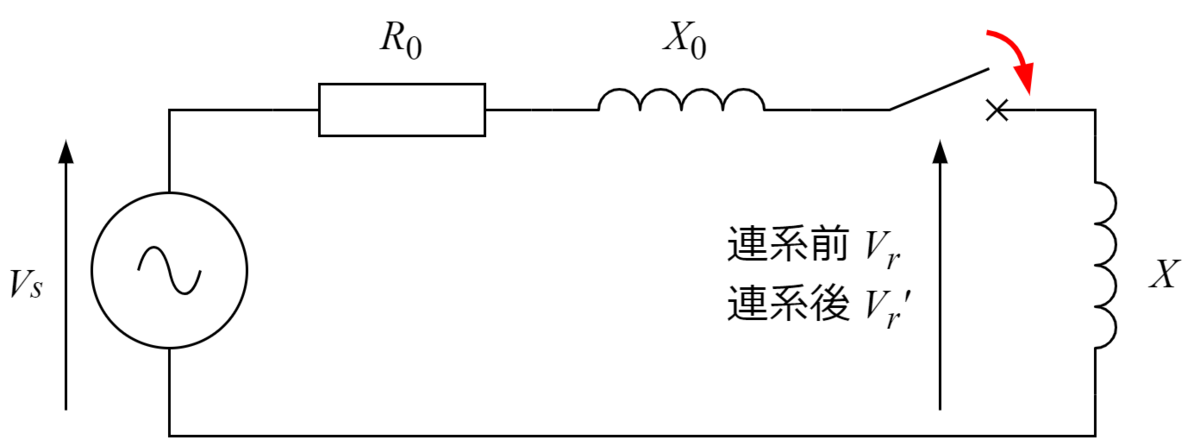
問4    分散型電源設置前後の電圧の導出に関する計算問題    配電
問5    中性点接地方式の目的と種類及び比較に関する論説問題    変電
問6    電力系統の周波数に関する計算・論説問題    電気施設管理

私は問3,4,5,6を選択しました。今回試験を受けたときにまず衝撃を受けたのは水力発電の問題が出題されたことでした。電験2種勢であればご存知の通り、水力、火力、水力、火力と毎年交互に出題されるのがこれまでのお決まりのパターンでした。去年は水力発電だったので、まさか今年に水力発電の問題が出題されるとは思っていませんでした。仕事柄、火力発電に関してはある程度の知識があったため楽観的に構えていて、水力の論説は全くフォローしていませんでした。よって問1はスルー。

問4,5は完全攻略にもあるオーソドックスな問題だったのでここで部分点が稼げたと思っています。問6の計算問題はOK、論説は×という感じです。あとは問2と問3で解けそうなほうで問3を選択しました。等面積法の計算は過去問をやってなかったので×でしたが、その手前の問題まではなんとか解きました。

手応えとしては120点中60～65点という感じでした。

機械・制御科目

問1    同期発電機の誘導起電力や電力，安定度に関する計算問題    同期機
問2    V結線した変圧器の各特性に関する計算問題    変圧器
問3    電力用能動フィルタに関する論説・計算問題    パワーエレクトロニクス
問4    ゲイン特性曲線からの伝達関数の導出に関する計算問題    自動制御

私は問1と問2を選択しました。全体的に前年度に比べて非常に難化した印象を持ちました。特に問4の制御は、ゲイン特性曲線から伝達関数を導出するトリッキーな問題。ブロック線図から伝達関数やゲイン特性を求めるいつもパターンとは異なり、初見で解くのは難しい印象でした。4、5分考えたけど無理そうなので切り替えて問1と問2にしました。制限時間60分のうちの4、5分ロスしてしまったのは非常に痛かったです。

問1は前半のベクトル図を導出して答えるところはOK、後半は×でした。時間に余裕あって落ち着いて考えたら後半も取れた感じがありました。

問2は完全攻略に載ってる問題（平成25年度）とほぼ同じでした。V結線変圧器の問題はベクトル図を描くのが難しいのですが、今回はベクトル図が問題に載っていたため幸い最後まで解くことができました。問2は全部正答取れました。

手応えとしては60点中45点という感じでした。機械・制御の計算問題にはかなりの自信があって、満点取って電力管理の点をカバーする気持ちだったのでこの結果は正直落ち込みました。

2科目合計で105～110点（58～61％）くらい。合格点の引き下げがあれば行ける？難化してるから引き下げあるかも？とわずかな期待感を持ちつつ合格発表を待っていました。結果は無事合格でしたが、今回合格できたのはかなり微妙なラインだったと思っています。

電験2種の勉強方法

私が実際にやった勉強方法を紹介します。

一次試験の勉強方法

一次試験対策は基本的にテキストと過去問が中心です。テキストは徹底マスターを使用していました。電験王で購入した過去問（PDFを印刷したもの）をひたすら解いていって、わからないところがあれば徹底マスターの該当箇所を読む、という感じです。最初は「これだけシリーズ」を購入しましたが内容が基礎的すぎて物足りなく感じたため徹底マスターを購入しました。機械・電力・法規の3種類を購入しました。理論は自信があったので参考書は不要でした。

電験二種徹底マスター 機械(改訂2版)

徹底マスターは細かいところまで解説がされていて非常に勉強になりました。二次試験を勉強する際にも使えるので持っておいて損はないです。試験が終わったあとも処分することはないと思います。

また、機械と電力を理解するためにYouTubeも活用しました。特にオススメなのはAki塾長さんのチャンネルです。電験3種用のチャンネルですが2種一次試験にも有効です。誘導機、同期機、直流機の動画の解説は非常に参考になります。

www.youtube.com

二次試験の勉強方法・計算問題

二次試験対策を始めるにあたって、まず以下の資料を一通り読みました。二次試験の範囲の内容がまとめられており二次試験が大体どんなものか理解できます。

電験2種2次 単元pdf置き場 | 電験3種「理論」最速合格

その後は皆さんお馴染みの不動先生の完全攻略を使用しました。二次試験の計算問題はこの本だけやってたらOKだと思います。自分も何周したのかわからないくらい解きまくりました。2回正答できた問題は飛ばして、間違えた問題をひたすら解いていくというやり方です。その結果、制御は現代制御以外バッチリという状態にまで仕上がりました。二次試験対策は完全攻略をやりまくった。これに尽きます。

電験二種完全攻略 二次試験対応(改訂2版): 過去問240問を体系的に学ぶ

二次試験の勉強方法・論説問題

論説問題対策には「キーワードで覚える」を購入しましたが結局あまり使わずじまいでした。

キーワードで覚える! 電験2種二次試験論説問題 改訂新版

自分の知らない内容を文字と図だけで覚えるのはやっぱりしんどいです。自分の業務に関わりある内容ならまだしも、水力発電とかケーブルの水トリーとか、見たことも扱ったこともない話は全く頭に入らないです。

そういうわけで二次試験の電力管理の対策については「論説問題は自分が知ってる内容だけはカバーしておく。それ以外は捨てる。計算問題で点を稼ぐ」という戦略にしました。論説問題も完全攻略に載っている内容しかフォローしていません。ノートを取ったり文字に書き起こしたりということもしませんでした。1回読んで理解できないものは諦めるというスタイルです💦

発電、送電、配電に関しては以下のYouTubeチャンネルがオススメです。YouTubeにある動画の中でもこの方の動画が一番詳しくて非常にわかりやすいです。

www.youtube.com

また、ノートに整理することはしませんでしたが、ブログには電験問題に関係する記事を継続して書いていました。それが論説対策の1つになったと思います。人に説明するために文章を書くという点ではブログに書く行為は非常に有効でした。

まとめ

以上が私の電験2種合格記です。今の時代はネットで良質な情報が無料で手に入って、良質な参考書もたくさん揃っているので本当にいい時代だと思います。Twitterで電験仲間を見つけることも勉強のモチベーションにもなります。わからない問題があってもTwitterに投稿すれば誰か（1種 or 2種保有者）が教えてくれる。本当に素晴らしいし、ありがたいです。電験の世界において「知の高速道路」が敷設されていることを身を持って実感します。この記事の内容がこれから電験2種を受けられる方の手助けになれば幸いです。

「超同期セルビウス方式」「二重給電誘導発電機」とは？

誘導機の速度制御の1つである超同期セルビウス方式について解説します。また、超同期セルビウス方式を使った例として、風力発電で用いられる二重給電誘導発電機 (DFIG) の動作について解説します。

超同期セルビウス方式

超同期セルビウス方式は二次励磁方式の1つです。二次励磁方式は巻線型誘導機をベースとしており、二次側（回転子巻線）が交流電源に繋がっているのが特徴です。一次側と二次側の両方から給電するので超同期セルビウス方式の誘導機を二重給電誘導機という言い方もします。同期速度以上での電動機運転が出来るので「超同期」セルビウス方式と言います。また、このは制御方式は発電機（特に風力発電）で使用されることが多いため、二重給電誘導発電機 や DFIG (Double-Fed Induction Generator) という呼ばれ方もします。

特徴

超同期セルビウス方式の特徴は①同期速度以上で誘導電動機として運転できること、②同期速度以下で誘導発電機として運転できることです。通常の誘導機だと同期速度以上では発電機、同期速度以下では電動機になりますが、超同期セルビウスでは二次周波数にすべり周波数の交流を印加することで、同期速度以上の電動機運転や同期速度以下の発電機運転を実現しています。

構成図

誘導発電機として運転するとき

超同期セルビウス方式の構成を以下に示します。以下は風力発電機（DFIG）の例です。

固定子側は通常の誘導機と同様に系統電源に接続されます。回転子側は系統電源から電力変換装置を経由して二次巻線に接続されます。電力変換装置としては一般的にサイクロコンバータが使用されます。サイクロコンバータからはスリップリングを経由して回転子巻線に繋がっています。DFIGにおいて機械的入力、一次電力、発電電力の向きは全て一方方向ですが、二次電力のみすべりの状態によって流れる方向が変化します。すべりが正（回転速度が同期速度より低い状態）のとき二次電力は系統電源から回転子巻線へ給電する方向に流れます。すべりが負（回転速度が同期速度を超えている状態）のとき二次電力は回生方向となり系統電源に向かって流れます。

損失を無視すると機械的出力 、一次電力 、二次電力 、発電電力 の関係は以下の式で表されます。

\begin{align} P_m = P_o \end{align} \begin{align} P_1 = \dfrac{P_m}{1 - s} \end{align} \begin{align} P_2 = \dfrac{s P_m}{1 -s} = sP_1 \end{align}

例として、すべりs=0.1とした場合、機械的入力を1とすると一次電力は1.11、二次電力は給電方向に0.11となります。トータルの発電電力は1.11 - 0.11 = 1であり機械的入力と等しいです。また、同期速度以上の場合、例えばすべりs = -0.1だと機械的入力1に対して一次電力は0.91、二次電力は回生方向に0.09です。

周波数に関しては、二次側回路の周波数＝すべり周波数です。DFIGでは回転速度と同期速度の差分を見て、すべり周波数に相当する周波数の励磁電流を電力変換装置から誘導機の二次側巻線に供給しています。

例えば極数4、周波数60Hzの誘導機で考えると同期速度は1800 rpm (60 Hz)です。もし発電機駆動軸の回転数が1500 rpmのときは、すべり周波数300 rpm、つまり10 Hzの交流を二次側に供給させます。これによって固定子の回転磁界は同期速度1800 rpmとなって系統の周波数と同期した状態になる、という仕組みです。DFIGでは風車の回転速度を常時検出し、それに応じた周波数を二次側に供給しています。ちなみに、すべりが負（回転速度が同期速度を超えている状態）においては二次側の回転磁界は逆方向（逆相）となります。

誘導電動機として運転するとき

超同期セルビウス方式の誘導機が電動機として動作するときの図を以下に示します。

電動機運転において二次電力の向きは、すべり正のとき回生方向、すべり負のとき給電方向となります。発電機のときと逆になりますので注意してください。

発電機のときと同様に二次側の回路の周波数はすべり周波数です。二次側に供給する励磁電流の周波数を変化させることで回転速度が変化する仕組みです。

等価回路を描いて動作原理を理解する

超同期セルビウス方式の誘導機を等価回路で考えてみます。まず誘導機の基本回路を以下に示します。

：一次側電圧（相電圧）、：二次側電圧（相電圧）
：一次側（固定子）抵抗、：一次側（固定子）リアクタンス
：二次側（回転子）抵抗、：二次側（回転子）リアクタンス

通常のかご型誘導電動機では二次側回路は短絡されていますが、二次励磁方式では二次側に交流電圧 を印加します。

二次側回路をsで割ります。

二次側回路の値を一次側に換算してT形等価回路にします。鉄損は無視し、励磁リアクタンスを とします。

普通の誘導機の等価回路と同じように二次側の抵抗 を銅損分 と機械的出力 に分けます。そして実は電圧も同様に と に分けることができます。後者は機械的エネルギーに相当します。

以下の図が超同期セルビウス方式のT形等価回路です。超同期セルビウス方式における機械的出力（または機械的入力）は赤色の破線箇所で示されます。

機械的出力（または機械的入力）は以下となります。

\begin{align}
P_m &= 3 \times \left( \dfrac{1-s}{s} R^{\prime}_{2} I^{\prime 2}_{2} + \mathrm{Re} \left[ \dfrac{1-s}{s} \dot{V^{\prime}_{2}} \overline {\dot I^{\prime}_{2}} \right] \right)
\\&= \dfrac{3(1-s)}{s} \left( R_{2} I^{2}_{2} + \mathrm{Re} \left[ \dot{V_{2}} \overline {\dot I_{2}} \right] \right)
\end{align}

が正のときは電動機、が負のときは発電機です。また、電圧と電流の位相をそれぞれ、とすると、

\begin{align}
P_m = \dfrac{3(1-s)}{s} \left\{ R_{2} I^{2}_{2} + V_{2} I_{2} \cos{( \phi_v - \phi_i )} \right\}
\end{align}

と表されます。二次電流 の位相と大きさは、上図のT形等価回路から重ね合わせの理を用いて二次電流（一次側換算） を求める必要がありますが、複雑な計算になるので今回は省略します。

まとめ

超同期セルビウス方式の概要と等価回路について説明しました。以上の内容より、超同期セルビウス方式では二次電流と二次側周波数を調整していることが理解できると思います。

参考サイト

• 富士電機 富士時報 第47巻第2号（1974年）

• 電験徒然草 54段 誘導電動機の二次励磁制御 ～二次抵抗制御時の損失を回収する～

火力発電プラントの制御方式（ボイラ追従方式、タービン追従方式、協調制御方式）

火力発電プラントのボイラ・タービンの制御方式には主にボイラ追従方式、タービン追従方式、ボイラ・タービン協調制御方式の3種類あります。その3種類を紹介します。これらの制御方式は火力発電プラントだけに限らずバイオマス発電プラントでも用いられます。

ボイラ追従方式 (Boiler-following mode)

概要

ボイラ追従方式は、発電機出力が出力目標値に一致するようにタービン蒸気加減弁の開度を調整し、一方でボイラ入力を調整して蒸気圧力を一定に保つ制御方式です。

例えば発電機の出力目標値を増やすと、出力制御コントローラが出力目標値 (SP) とタービン発電機の出力 (PV) の偏差を見て、蒸気加減弁を開方向に動かします。この結果、発電機の出力は増加します。このときボイラ入力と蒸気流量のバランスが一時的に崩れるのでボイラの蒸気圧力は低下します。そこで今度は圧力コントローラが圧力設定値 (SP) と測定値 (PV) の偏差を見てボイラ入力を増加させます。以上がボイラ追従方式の動作のイメージです。出力目標値を下げた場合は逆の動作が起こります。ちなみに、ここで言うボイラ入力とは燃料 (Fuel) と空気 (Air) と給水 (Feedwater) のことを指します。ただし、ドラム形ボイラにおいては給水流量はドラムレベル制御によって操作されるので、ボイラ入力で操作されるのは燃料投入量と空気供給量の2つとなります。

長所

ボイラ追従方式の利点は出力目標値の変化や負荷変動に対する応答性が早い点にあります。なぜならタービン入口の蒸気加減弁を調整するためです。

短所

ボイラ追従方式は後述のタービン追従方式に比べて負荷変化時のボイラの変動が大きいです。したがってボイラ追従方式は一般的にドラム形ボイラに採用されます。ドラム形ボイラは蓄熱容量が大きく、負荷変動に対する蒸気圧力が小さい特徴を持っています。負荷が変動してもボイラは比較的安定的なのでドラム形ボイラとボイラ追従方式は相性が良いです。一方、貫流ボイラは蓄熱容量が小さいため、もし仮に貫流ボイラにボイラ追従方式の制御を適用するとボイラが不安定になって制御は大変困難になると予想されます。

タービン追従方式 (Turbine-following mode)

概要

タービン追従方式では、タービン発電機の出力制御は蒸気加減弁ではなくボイラ燃料供給量によって調整を行います。蒸気加減弁は蒸気圧力を一定に保つ役割を担います。

上の図で示しているように、発電機出力制御コントローラの出力MVはボイラ燃料供給量の目標値となります。例えば出力目標値を増やすと出力制御コントローラはボイラの燃料供給量を増加させます。ボイラ入力が増えるとボイラの圧力が上昇します。このとき圧力コントローラが蒸気設定値と測定値の偏差を見て蒸気加減弁を開動作させます。これらの結果として蒸気圧力は一定を保ちながら発電機の出力は増加します。

長所

ボイラ主体で制御を行うため、ボイラ追従方式に比べるとボイラ側は安定します。

短所

タービン入口の蒸気加減弁ではなくボイラ燃料の投入量によって負荷制御を行うので、制御にラグが発生します。そのため負荷追従性はボイラ追従方式に比べて悪くなります。したがってタービン追従方式は負荷追従性が高い貫流ボイラに採用されます。

ドラム形ボイラと貫流ボイラの特徴をまとめると以下のようになります。

ドラム形ボイラ：負荷追従性が遅い。負荷の変動に対してボイラの変動が小さい。→ボイラ追従方式で制御する。

貫流ボイラ：負荷追従性が早い。負荷の変動に対してボイラの変動が大きい。→タービン追従方式で制御する。

ボイラ追従方式とタービン追従方式は、それぞれのボイラの短所をカバーして長所をうまく利用する制御というイメージです。

ボイラ・タービン協調制御方式 (Coordinated control mode)

ボイラ・タービン協調制御方式とは、言わばボイラ追従方式とタービン追従方式のいいとこ取り制御です。簡単な図で表すと以下のような感じになります。

蒸気加減弁とボイラ入力を同時並行で制御します。どちらかが他方に追従するわけではないです。両方を同時にうまく調整することでボイラ追従方式とタービン追従方式それぞれの欠点を取り除いています。詳細の制御ループは以下のようになります。※簡略化していますが実際はもっと複雑です。

タービン蒸気加減弁は出力制御コントローラによって制御されます。一方で燃料の投入量制御は少し複雑です。まず発電機出力目標値に主蒸気圧力制御のMVを加算したものをボイラマスタ信号と言います。実際のプラントにおいては負荷追従性をより改善するために、ボイラマスタ信号には出力目標値や圧力制御の他、フィードフォワード制御が使われたりします。

次に燃料関数を用いて、ボイラへ投入する燃料の目標値を決定します。その目標値に追従するようにボイラに燃料が投入されます。燃焼空気のほうは空燃比関数を使って燃料投入量目標値に応じて燃焼空気流量の目標値が決定されます。その空気流量目標値に追従するように燃焼空気が制御されます。ちなみにボイラの燃焼制御においてはクロスリミット制御が使用されます。今回説明は省略しますが、クロスリミット制御を行うことで負荷変化時の過渡状態においても空燃比が適正な範囲内で維持されるよう制御されます。

協調制御方式は負荷追従性が高く、ボイラ側も安定するため特に大規模な火力発電プラントに使用されます。あえて協調制御方式の欠点を挙げるならば、ボイラ追従方式やタービン追従方式に比べて制御ループの構成が複雑になるため、パラメータ調整が難しいという点でしょうか。

参考リンク

• Boiler-Tuning Basics, Part II
• Improving Boiler Stability Through Advanced Regulatory Control （PDFファイル）

• 計装豆知識｜クロスリミット制御

瞬時電圧低下率の検討と限流リアクトルの計算例

以下の記事では誘導発電機の並列時の瞬時電圧低下率について解説しました。

electrical-instrumentation.com

今回は、瞬時電圧低下率を検討する目的と瞬時電圧低下率抑制の計算方法について解説してみます。

瞬時電圧低下率を検討する目的と許容範囲

なぜ瞬時電圧低下率を計算するのかと言うと、瞬時電圧低下率が許容範囲内に収まっているかを確認するためです。発電設備並列時の瞬時電圧低下に関しては電力品質確保に係る系統連系技術要件ガイドラインに以下の記載があります。

発電等設備の連系時の検討においては、発電等設備の並解列時の瞬時電圧低下は、コンピュータ、OA機器、産業用ロボット等の情報機器が、定格電圧の10％以上の瞬時電圧低下により機器停止等の影響を受ける場合があることも勘案し、常時電圧の10％以内（100V系では90Vが下限値）とすることが適切である。

要するに、発電機並列時の瞬時電圧低下が大きすぎると電子機器の動作に影響が出るので、瞬時電圧低下率は常時電圧の10％以内に抑えましょうという内容です。言い換えれば発電機を並列した瞬間の電圧が、常時電圧の90％以上である必要があります。また、誘導発電機連系時の瞬時電圧低下が10％を超える場合においては、限流リアクトル等の設置が求められます。これもガイドラインに記載があります。

ちなみに10％以内というのは高圧配電線に連系する場合であり、特別高圧においては2％以内が目安となります。

例題

限流リアクトルがない場合

誘導発電機連系点における瞬時電圧低下率の計算式は以下の通りです。 が発電機から見た系統側の％インピーダンス、 は誘導発電機の拘束リアクタンスです。

\begin{align}
\varepsilon = 1 - \dfrac{X}{\sqrt{R_0^2 + (X_0 + X)^2}}
\end{align}

電験2種二次試験の過去問題では でしたが、例えば誘導発電機の拘束リアクタンスを に変えて計算してみると電圧低下率は以下のようになります。

\begin{align}
\varepsilon = 1 - \dfrac{250}{\sqrt{16.15^2 + (36.45 + 250)^2}} = 0.129
\end{align}

瞬時電圧低下率は12.9％となり、ガイドラインで要求される10％を逸脱します。瞬時電圧低下率を抑制するためには限流リアクトルの設置が必要となります。次に、この条件において、連系条件を満足するために必要な限流リアクトルの値を求めてみます。

限流リアクトルを設置した場合

限流リアクトルを とすると、発電機連系点における瞬時電圧低下率の計算式は以下のようになります。

\begin{align}
\varepsilon = 1 - \dfrac{X + X_1}{\sqrt{R_0^2 + (X_0 + X + X_1)^2}}
\end{align}

瞬時電圧低下率を10％以内にするためには、以下が成立しなければなりません。

\begin{align}
1 - \dfrac{250 + X_1}{\sqrt{16.15^2 + (36.45 + 250 + X_1)^2}} \leqq 0.1
\end{align}

この2次方程式を解くと となり、基準容量ベースで81％以上のリアクタンスを持つ限流リアクトルを設置すれば連系条件を満足することになります。電験の本番では2次方程式を手計算で頑張って解かないとダメですが、Excelで計算すれば簡単です（笑）

まとめ

誘導発電機を並列した際の瞬時電圧低下率の許容値と、限流リアクトルの計算例を紹介しました。限流リアクトルによる電圧低下の抑制に関しては過去に平成6年度の電験1種二次試験で出題されています。今後、電験2種の二次試験で出題される可能性も、もしかしたらあるかもしれません。

参考文献

電力品質確保に係る系統連系技術要件ガイドライン, 令和5年4月1日, 資源エネルギー庁 （PDFファイル）

電験_配電線No9_風力発電接続時の限流リアクトルによる電圧降下の抑制（ 1種 送配電−平成6年−問題3） - Ubuntu，Lubuntu活用方法，電験１種・２種取得等の紹介ブログ

電力用コンデンサ投入時の電圧変動率

誘導発電機を系統に連系した際に生じる瞬時電圧低下率について、電験2種の過去問を問いてみます。誘導発電機を系統に連系した際に生じる瞬時電圧低下率について、電験2種の過去問を問いてみます。

コンデンサ投入時の母線電圧の電圧変動率について、電験2種の過去問を解いてみます。電験王と不動先生の完全攻略の解法では初見では解けなさそうだったので自分なりに解いてみます。

平成29年 電験2種二次試験 電力・管理 問3

図のような一次側が ，二次側が の変圧器3台で連系された変電所がある。この変電所の 側母線に接続された の電力用コンデンサを投入したとき，次の問に答えよ。なお，各変圧器のインピーダンスはリアクタンスのみとし，その値は自己容量基準で図に示すとおりである。

(1) 母線の短絡容量 を求めよ。なお，単位法における基準容量は として計算せよ。

(2) 電力用コンデンサを投入したときの 側母線の基準電圧に対する電圧変動率 を求めよ。

(3) 電力用コンデンサを投入したときの 側母線の基準電圧に対する電圧変動率 を求めよ。

77 [kV] 母線の短絡容量 Ps [MV・A]

以下の赤字のように適当に記号を振って、等価回路を作ると以下の図のようになります。

まずは全体の合成インピーダンス を計算します。その後、基準容量 との関係から は以下のように算出できます。単純計算なので計算過程は省略します。

\begin{align}
\% Z = 4.0708 \, \lbrack \% \rbrack
\end{align}

\begin{align}
P_S &= \dfrac{100}{\% Z} \times P_n  \\&= 2456.6 \fallingdotseq 2460 \, \lbrack \mathrm{MV \cdot A} \rbrack
\end{align}

コンデンサ投入時の 77 kV 母線の電圧変動率

2通りの解き方を記載します。

1. 電圧降下の計算式を使った解法
2. インピーダンスの分圧計算を使った解法

電圧降下の計算式（単位法）を使った解法

コンデンサ投入後の 母線の電圧を とします。また、基準電圧は とします。以降、単位法で解いていきます。コンデンサ投入前は電流が流れていないので 母線の電圧は   です。電圧変動率 は単位法の電圧降下の式より

\begin{align}
\Delta V = V_B - V_{77} = \dfrac{RP+XQ}{V_{77}}  \, \lbrack \mathrm{p.u.} \rbrack 
\end{align}

となる。ちなみに と仮定して分母を1にするパターンもあるが、とりあえずこのまま解く。問題に抵抗分、有効電力は存在せず、、なので（進相無効電力なので負）

\begin{align}
1 - V_{77} = \dfrac{- 0.040708 \times 0.3}{V_{77}} 
\end{align}

この2次方程式を解くと、

\begin{align}
V_{77} = 1.01206 \, \lbrack \mathrm{p.u.} \rbrack
\end{align}

となる。よって電圧変動率 は

\begin{align}
\Delta V_{77} = 1 - 1.01206 = -0.01206  \, \lbrack \mathrm{p.u.} \rbrack
\end{align}

母線電圧 は基準電圧 より大きい。上記で用いた式は電圧降下の式なので計算結果に負の符号が付いているということは、コンデンサ投入後は母線電圧が上昇していることを意味する。負荷がないのでフェランチ効果によって電圧上昇しているイメージ。今回、上昇 or 低下は問われていないので解答としては以下のようになります。

\begin{align}
\Delta V_{77} \fallingdotseq 1.21 \, \lbrack \% \rbrack
\end{align}

ちなみに、もし として分母を1として近似計算した場合、計算結果は以下の値となります。

\begin{align}
\Delta V_{77} \fallingdotseq 1.22 \, \lbrack \% \rbrack
\end{align}

インピーダンスの分圧計算を使った解法

等価回路からインピーダンスの分圧計算で解くやり方です。合成インピーダンス とコンデンサのインピーダンス で表した等価回路は以下の図となります。

のコンデンサのインピーダンスを ベースのPUインピーダンスに変換すると となる。等価回路より 母線電圧 は、

\begin{align}
V_{77} &= \dfrac{Z_C}{Z + Z_C} V_B \\&= \dfrac{ - j \frac{100}{30}}{j0.040708 - j \frac{100}{30}} \times 1 \\&= 1.01236  \, \lbrack \mathrm{p.u.} \rbrack
\end{align}

となる。よって、電圧変動率は以下の値となります。

\begin{align}
\Delta V_{77} \fallingdotseq 1.24 \, \lbrack \% \rbrack
\end{align}

コンデンサ投入時の 154 kV 母線の電圧変動率

母線の電位を等価回路で示すと赤のポイントとなります。

また、 母線における電圧変動率 と 母線における電圧変動率 は青で示したイメージとなる。 から構成される並列インピーダンスを とおくと は以下の通り。※並列インピーダンスの計算過程は省略。

\begin{align}
\Delta V_{154} &= \dfrac{Z_1}{Z_1 + Z_T} \Delta V_{77} \\&= \dfrac{2}{2 + 3.1111} \times 1.206 \\&= 0.4719 \fallingdotseq 0.472 \, \lbrack \% \rbrack
\end{align}

上記の式において は1つ目の解き方で求めた値を使用しています。

考察

2通りの解き方で 母線における電圧を求めてみました。どちらも等価回路をちゃんと作って考えるのがポイントです。

どちらがより正確か？と言うと1つ目のやり方のほうが真値に近いと思います。なぜ計算結果に差が出るのか？ 2つ目のやり方では、コンデンサのインピーダンスを単位法で表していますが、これが誤差が生じる理由なのかなと思っています。コンデンサをPUインピーダンスで表す場合、コンデンサの電圧（母線電圧）は基準電圧に等しいという前提がありますが、これが誤差の要因になってくるんじゃないかと。まぁ、電圧変動率の計算結果は小数点第1位まで合ってたら正解としてほしいです。

参考サイト

1つ目のリンク先は完全攻略や公式解答と同じ解き方です。下のリンク先は本記事の1つ目と同じ解き方です。

denken-ou.com

den1-tanaoroshi.com

誘導発電機連系時の瞬時電圧低下率

誘導発電機を系統に連系した際に生じる瞬時電圧低下率について、電験2種の過去問を問いてみます。

平成22年 電験2種二次試験 電力・管理 問4

図のような高圧配電系統で，誘導発電機を連系した際，次の問に答えよ．

ただし，基準容量 におけるアルミ電線 の％インピーダンスは 当たり ，アルミ電線 の％インピーダンスは 当たり とする．

(1) 基準容量 において，配電系統との連系点からみた系統側の％インピーダンスを とした場合， ， の値をそれぞれ求めよ．

(2) 基準容量 において，誘導発電機の拘束インピーダンスはリアクタンス成分のみとし，これを とした場合， の値を求めよ．

(3) 誘導発電機の連系によって発生する，配電系統との連系点における瞬時電圧低下率を求めよ．なお，配電系統との連系点から誘導発電機端までのインピーダンスおよび誘導発電機の抵抗分は無視する．

(1) 連系点から見た系統側の％インピーダンス

\begin{align}
R_0 + j X_0 = 16.15 + j 36.45 \, \lbrack \% \rbrack
\end{align}

ただの四則演算なので計算は省略します。

(2) 誘導発電機の拘束リアクタンス

\begin{align}
X = 20 \times \dfrac{10 000}{500} = 400 \, \lbrack \% \rbrack
\end{align}

400 kW を力率0.8で割って 500 kVA に変換します（これが重要）。そして、％インピーダンスを 10 MVA に換算すればOKです。

(3) 配電系統との連系点における瞬時電圧低下率

等価回路は以下のようになります。誘導発電機のリアクタンス に生じる電圧が連系点における電圧となります。

系統の電源電圧を 、連系点の電圧は連系前を 、連系後を とする。連系前後の電圧を比較し、電圧低下率を求める。

連系前

連系前は電流が流れていないので以下の関係が成り立つ。連系点における電圧は系統電源電圧に等しい。

\begin{align}
V_r = V_s
\end{align}

連系後

誘導発電機連系後の連系点における電圧は、分圧計算で以下の通り。

\begin{align}
V_r' &= \dfrac{X}{\sqrt{R_0^2 + (X_0 + X)^2}} V_s \\ &= \dfrac{400}{\sqrt{16.15^2 + (36.45 + 400^2)}} V_s \\ &= 0.9159 V_s
\end{align}

これは「誘導発電機連系後の連系点における電圧は系統電源電圧の91.59％である」という意味。ここまでわかればもう正解できたようなもんです。

瞬時電圧低下率

連系前の関係式 より連系前後の連系点電圧は以下のようになる。

\begin{align}
V_r’ = 0.9159 V_r
\end{align}

よって、瞬時電圧低下率 は以下の通り。

\begin{align}
\varepsilon &= \dfrac{V_r - V_r'}{V_r} \\ &= \dfrac{V_r - 0.9159 V_r}{V_r} \\ &= 1 - 0.9159 \\ &= 0.0841 = 8.41 \, \lbrack \% \rbrack
\end{align}

まとめ

誘導発電機の瞬時電圧低下率を分圧計算を使って計算してみました。テキストの解説では、電圧＝電流×インピーダンス で電圧を求める例がありますが、実際は分圧計算で求めるのがシンプルでわかりやすいかと思います。

この計算方法は、実は誘導電動機の始動時の電圧低下の計算方法と全く同じです（以下の記事参照）。等価回路を作って、求めたい箇所の電圧を分圧計算で求めて、その値が基準よりいくら下がっているか？という考え方です。

electrical-instrumentation.com

系統周波数が上がると消費電力が増加する？

系統の負荷の周波数特性について疑問に思った話と解決した話をメモします。

電験のテキストには負荷の周波数特性について以下の内容が書かれています。

「負荷は周波数が上がると消費電力が増加し、周波数が下がると消費電力が減少する特性がある。負荷の周波数特性定数を とすると周波数変化量 に対する消費電力変化量 は以下の式で表される。」

\begin{align}
\Delta P_L = K_L \Delta f
\end{align}

平成23年の電験2種二次試験（電力・管理）にこの内容が出題されています。

denken-ou.com

上の文章を読んだとき自分は全く理解できませんでした。「負荷が変動したら需給バランスが崩れるから周波数が変動するんじゃないの？逆に周波数の変化で電力が変わることってある？」と思ってました。

ネットで調べてみても、どれも「そういう特性がある」と書いてあるだけで納得のいく説明が見つかりませんでした。そのことをツイッターに投稿したところ一瞬で解決しました。

世の中の負荷の半分弱は誘導電動機であり、誘導電動機の消費電力が周波数に影響を受けるからだと思います。

— がえ@電力🌊 (@photovoltic555) 2023年1月29日

世の中の負荷の半分くらいは電動機（回転機器）です。電動機の動力は系統周波数に依存するので、周波数の変化すると負荷の消費電力が変わるということです。消費電力が系統周波数によって変化する理由は、電動機の軸動力が変わるからなんですね。

電動機の軸動力 は トルク と 角速度 より以下の式で表されます。

\begin{align}
P = T \omega
\end{align}

角速度（回転速度）は系統周波数に依存します。なので、系統周波数が変化すると電動機の軸動力が変わって消費電力が変化するということです。これは電動機一般の話なので誘導電動機も同期電動機も同じ話です。ちなみにポンプやファンなどの2乗低減トルク負荷はトルクが回転速度の2乗に比例するので動力 は周波数の3乗に比例します。

「負荷が変動したら周波数が変化する」というのは発電機の立場で考えた場合の話ですね。例えば系統の負荷の一部が脱落したとするとその瞬間、発電＞負荷の状態になるので発電機の回転数が上がる。その結果、周波数が増加する、というイメージです。