
コンデンサ投入時の母線電圧の電圧変動率について、電験2種の過去問を解いてみます。電験王と不動先生の完全攻略の解法では初見では解けなさそうだったので自分なりに解いてみます。
- 平成29年 電験2種二次試験 電力・管理 問3
- 77 [kV] 母線の短絡容量 Ps [MV・A]
- コンデンサ投入時の 77 kV 母線の電圧変動率
- コンデンサ投入時の 154 kV 母線の電圧変動率
- 考察
- 参考サイト
平成29年 電験2種二次試験 電力・管理 問3
図のような一次側が ,二次側が
の変圧器3台で連系された変電所がある。この変電所の
側母線に接続された
の電力用コンデンサを投入したとき,次の問に答えよ。なお,各変圧器のインピーダンスはリアクタンスのみとし,その値は自己容量基準で図に示すとおりである。
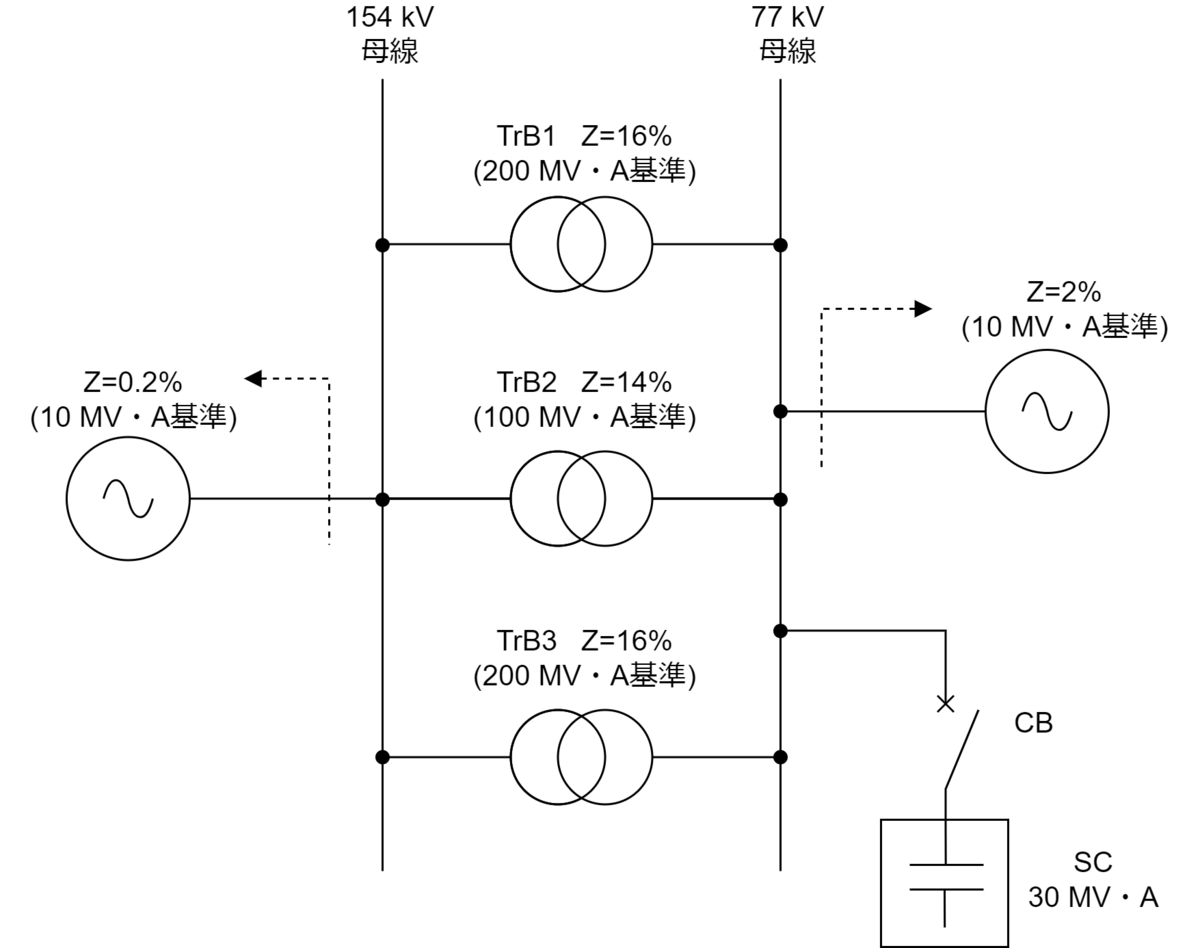
(1) 母線の短絡容量
を求めよ。なお,単位法における基準容量は
として計算せよ。
(2) 電力用コンデンサを投入したときの 側母線の基準電圧に対する電圧変動率
を求めよ。
(3) 電力用コンデンサを投入したときの 側母線の基準電圧に対する電圧変動率
を求めよ。
77 [kV] 母線の短絡容量 Ps [MV・A]
以下の赤字のように適当に記号を振って、等価回路を作ると以下の図のようになります。


まずは全体の合成インピーダンス を計算します。その後、基準容量
との関係から
は以下のように算出できます。単純計算なので計算過程は省略します。
\begin{align}
\% Z = 4.0708 \, \lbrack \% \rbrack
\end{align}
\begin{align}
P_S &= \dfrac{100}{\% Z} \times P_n \\&= 2456.6 \fallingdotseq 2460 \, \lbrack \mathrm{MV \cdot A} \rbrack
\end{align}
コンデンサ投入時の 77 kV 母線の電圧変動率
2通りの解き方を記載します。
- 電圧降下の計算式を使った解法
- インピーダンスの分圧計算を使った解法
電圧降下の計算式(単位法)を使った解法
コンデンサ投入後の 母線の電圧を
とします。また、基準電圧は
とします。以降、単位法で解いていきます。コンデンサ投入前は電流が流れていないので
母線の電圧は
です。電圧変動率
は単位法の電圧降下の式より
\begin{align}
\Delta V = V_B - V_{77} = \dfrac{RP+XQ}{V_{77}} \, \lbrack \mathrm{p.u.} \rbrack
\end{align}
となる。ちなみに と仮定して分母を1にするパターンもあるが、とりあえずこのまま解く。問題に抵抗分、有効電力は存在せず、
、
なので(進相無効電力なので負)
\begin{align}
1 - V_{77} = \dfrac{- 0.040708 \times 0.3}{V_{77}}
\end{align}
この2次方程式を解くと、
\begin{align}
V_{77} = 1.01206 \, \lbrack \mathrm{p.u.} \rbrack
\end{align}
となる。よって電圧変動率 は
\begin{align}
\Delta V_{77} = 1 - 1.01206 = -0.01206 \, \lbrack \mathrm{p.u.} \rbrack
\end{align}
母線電圧 は基準電圧
より大きい。上記で用いた式は電圧降下の式なので計算結果に負の符号が付いているということは、コンデンサ投入後は母線電圧が上昇していることを意味する。負荷がないのでフェランチ効果によって電圧上昇しているイメージ。今回、上昇 or 低下は問われていないので解答としては以下のようになります。
\begin{align}
\Delta V_{77} \fallingdotseq 1.21 \, \lbrack \% \rbrack
\end{align}
ちなみに、もし として分母を1として近似計算した場合、計算結果は以下の値となります。
\begin{align}
\Delta V_{77} \fallingdotseq 1.22 \, \lbrack \% \rbrack
\end{align}
インピーダンスの分圧計算を使った解法
等価回路からインピーダンスの分圧計算で解くやり方です。合成インピーダンス とコンデンサのインピーダンス
で表した等価回路は以下の図となります。

のコンデンサのインピーダンスを
ベースのPUインピーダンスに変換すると
となる。等価回路より
母線電圧
は、
\begin{align}
V_{77} &= \dfrac{Z_C}{Z + Z_C} V_B \\&= \dfrac{ - j \frac{100}{30}}{j0.040708 - j \frac{100}{30}} \times 1 \\&= 1.01236 \, \lbrack \mathrm{p.u.} \rbrack
\end{align}
となる。よって、電圧変動率は以下の値となります。
\begin{align}
\Delta V_{77} \fallingdotseq 1.24 \, \lbrack \% \rbrack
\end{align}
コンデンサ投入時の 154 kV 母線の電圧変動率
母線の電位を等価回路で示すと赤のポイントとなります。

また、 母線における電圧変動率
と
母線における電圧変動率
は青で示したイメージとなる。
から構成される並列インピーダンスを
とおくと
は以下の通り。※並列インピーダンスの計算過程は省略。
\begin{align}
\Delta V_{154} &= \dfrac{Z_1}{Z_1 + Z_T} \Delta V_{77} \\&= \dfrac{2}{2 + 3.1111} \times 1.206 \\&= 0.4719 \fallingdotseq 0.472 \, \lbrack \% \rbrack
\end{align}
上記の式において は1つ目の解き方で求めた値を使用しています。
考察
2通りの解き方で 母線における電圧を求めてみました。どちらも等価回路をちゃんと作って考えるのがポイントです。
どちらがより正確か?と言うと1つ目のやり方のほうが真値に近いと思います。なぜ計算結果に差が出るのか? 2つ目のやり方では、コンデンサのインピーダンスを単位法で表していますが、これが誤差が生じる理由なのかなと思っています。コンデンサをPUインピーダンスで表す場合、コンデンサの電圧(母線電圧)は基準電圧に等しいという前提がありますが、これが誤差の要因になってくるんじゃないかと。まぁ、電圧変動率の計算結果は小数点第1位まで合ってたら正解としてほしいです。
参考サイト
1つ目のリンク先は完全攻略や公式解答と同じ解き方です。下のリンク先は本記事の1つ目と同じ解き方です。