スターデルタ始動モータの電圧降下計算 - プラント電気計装エンジニアのメモ

スターデルタ始動モータのケーブルの電圧降下について解説します。

直入れ三相モータの電圧降下計算式
スターデルタ始動モータの電圧降下計算式
- Δ結線時（定常時）
- Y結線時（始動時）
まとめ

直入れ三相モータの電圧降下計算式

まず基本式として、直入れの三相モータの電圧降下計算式は以下の通りです。

$\Delta V = \sqrt{3} I L ( R \cos{\theta} + X \sin{\theta} )$

ΔV：ケーブルに生じる電圧降下 [V]
I：負荷電流 [A]
L：配線距離 [km]
R：ケーブルの抵抗 [Ω/km]
X：ケーブルのリアクタンス [Ω/km]
cosθ：負荷力率　※ $\sin{\theta} = \sqrt{1 - \cos^{2}{\theta}}$

上式が使えるのは直入れの三相モータやインバータ始動の場合です。スターデルタ始動では配線が6本になるのでこの式は使えません。

スターデルタ始動モータの電圧降下計算式

スターデルタの場合、制御盤からモータ端子部までのケーブルで発生する電圧降下の計算式は以下の式となります。

$\Delta V = \dfrac{2}{\sqrt{3}} I L ( R \cos{\theta} + X \sin{\theta} )$

直入れの基本式とは右辺第1項の係数が異なります。なぜこうなるかを以下で解説します。

Δ結線時（定常時）

まずは通常運転時のΔ結線で考えてみます。スターデルタ始動の回路を以下に示します。

Δ結線はMCとMCDが閉、MCSが開の状態です。U-Y, V-Z, W-Xがそれぞれ短絡状態となり、モータの回路は以下のようになります。

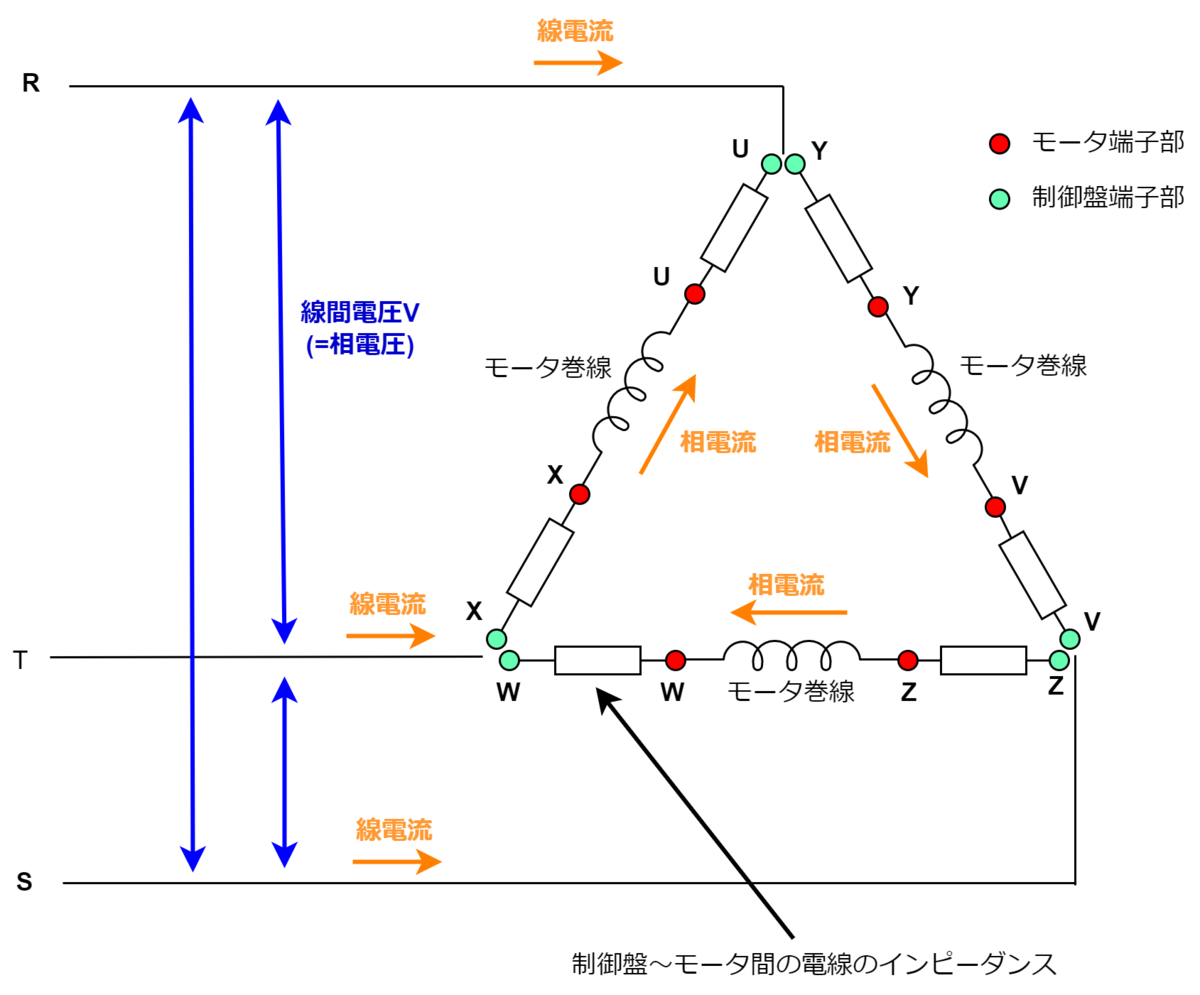
スターデルタ始動では配線が6本あるのでインピーダンスは2倍となります。言い換えると、制御盤からモータまでの距離がLの場合、インピーダンスは（単位長さあたりの電線インピーダンス）×2Lとして計算する必要があります。

また、電線を流れる電流は線電流ではなく相電流であることに注意してください。相電流は線電流の1／√3倍です。よって負荷電流I (A)流れているとき、実際のケーブルには I／√3 の電流が流れています。

以上より、ケーブル長さLが2倍、電流Iが1／√3倍になるということで、電圧降下の計算式は以下の式となります。

$\Delta V = \dfrac{2}{\sqrt{3}} I L ( R \cos{\theta} + X \sin{\theta} )$

直入れモータの違いは、直入れの場合は線電流のところでケーブルの電圧降下を計算しますが、スターデルタのΔ結線では相電流のところで電圧降下を計算する点にあります。相電流（相電圧）のところで見ているので三相モータの基本式にあった係数√3は今回関係なく、係数は2／√3となります。

Y結線時（始動時）

始動時すなわちY結線時の回路は以下の通りとなります。

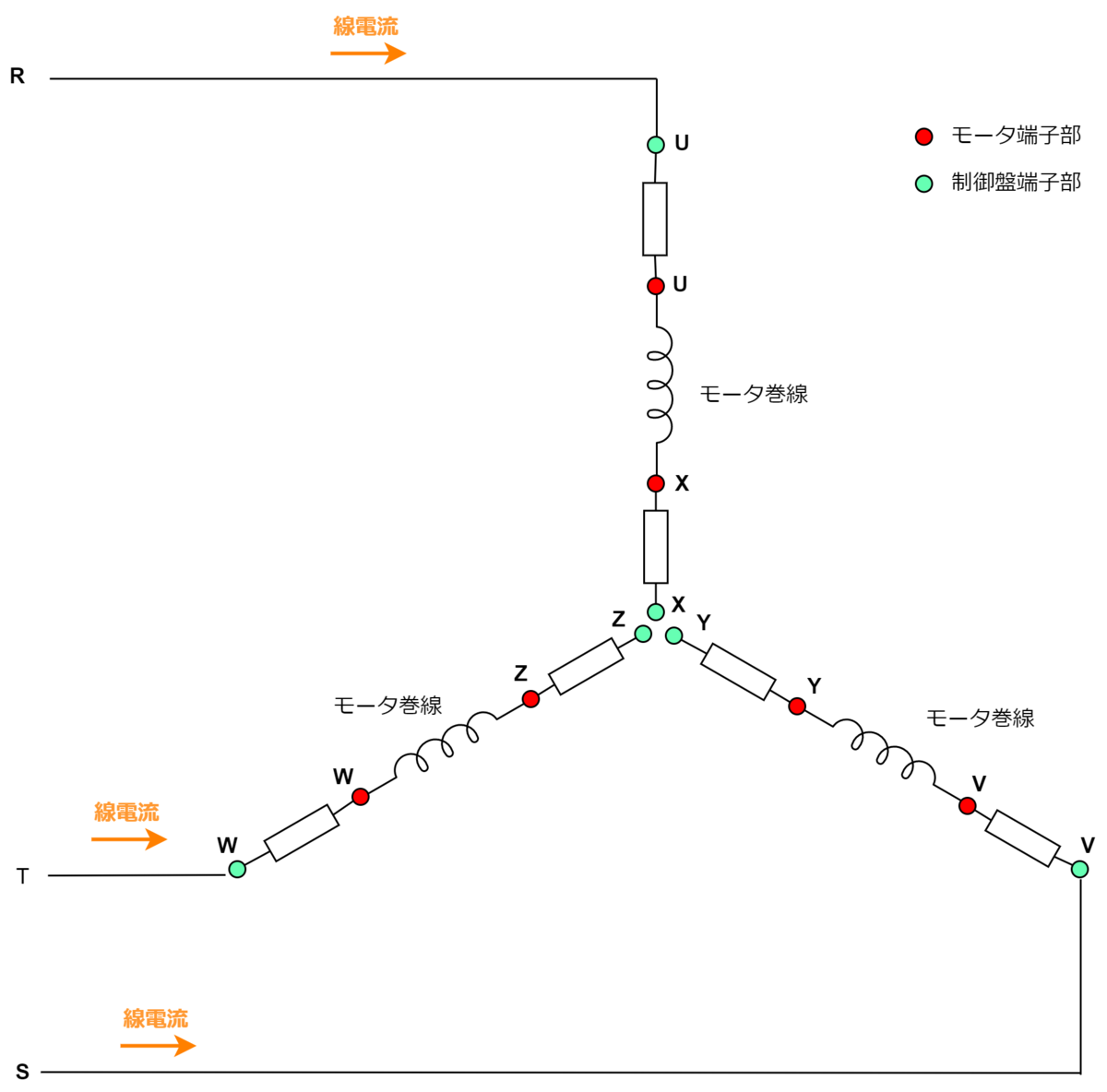
直入れ時と比較して、ケーブルの長さが2倍になるのでL→2Lとします。また、スターデルタ始動におけるY結線では電流がΔ結線時の1／3倍となりますので、I→I／3とします。Y結線時の電圧降下は、基本式を用いて以下の式となります。

$\Delta V = \dfrac{2}{3} \times \sqrt{3} I L ( R \cos{\theta} + X \sin{\theta} )$

$\dfrac{2}{3} \times \sqrt{3} = \dfrac{2}{\sqrt{3}}$ ですのでΔ結線時のときに求めた計算式と同様の式になります。ちなみに上の式での電流Iは直入れ時の始動電流（例えば定格電流の10倍）です。

以上より、スターデルタでは始動時の電圧降下は直入れ時の2／3倍（67％）になることがわかります。ただし、直入れとスターデルタでは電線サイズも変わってくると思いますので一概に2／3倍になるというわけではないです。あくまでざっくりとしたイメージとして。始動電流が1／3倍になるからと言って電圧降下が1／3倍になるわけではないです！